This webpage contains the following sections:
- Introduction
- Steps required: overview and comparison to the linear case (this contains a summary of differences from the linear case at the end of the section; make sure you read it).
- Difficult steps: detailed explanations and examples. This section focuses on 2 skills:
- how to choose the pivot point
- how to find the expression for a torque. This subsection is in turn divided into the 3 skills required:
- figure out whether the torque is positive or negative (for your choices of + direction and pivot point).
- write down the magnitude of the force that creates the torque
- figure out the lever arm (for your choice of pivot point).
- More practice/diagnostic example (starts about 3 quarters of the way down). If you already have a fair amount of practice with these problems, you may want to start there. Do what is asked there, and you should be able to tell whether you are lacking some critical skills, and where to do on this page to acquire them.
The law which involves torques is the angular version of Newton's 2nd law. Recall that Newton's 2nd law in its usual, linear form tells you that the linear acceleration of an object is due to all the forces acting on this object: the object accelerates if there is a net force acting on it, and the larger its mass the less it accelerates:
- Introduction
- Steps required: overview and comparison to the linear case (this contains a summary of differences from the linear case at the end of the section; make sure you read it).
- Difficult steps: detailed explanations and examples. This section focuses on 2 skills:
- how to choose the pivot point
- how to find the expression for a torque. This subsection is in turn divided into the 3 skills required:
- figure out whether the torque is positive or negative (for your choices of + direction and pivot point).
- write down the magnitude of the force that creates the torque
- figure out the lever arm (for your choice of pivot point).
- More practice/diagnostic example (starts about 3 quarters of the way down). If you already have a fair amount of practice with these problems, you may want to start there. Do what is asked there, and you should be able to tell whether you are lacking some critical skills, and where to do on this page to acquire them.
INTRODUCTION
The law which involves torques is the angular version of Newton's 2nd law. Recall that Newton's 2nd law in its usual, linear form tells you that the linear acceleration of an object is due to all the forces acting on this object: the object accelerates if there is a net force acting on it, and the larger its mass the less it accelerates:
Σ F→ = m . a→
The angular version of Newton's 2nd law tells you that the angular acceleration of an object is due to all the torques acting on this object: it accelerates in its rotation, in its spin, if there is a net torque acting on it, and the larger its moment of inertial, the less it accelerates in its rotation:
Σ τ→ = I . α→
STEPS REQUIRED:
OVERVIEW AND COMPARISON TO THE LINEAR CASE
Recall that when you apply the linear version of Newton's 2nd law, you need to:
1) Write down Σ F→ = m . a→
3) Draw a free body diagram: i.e. draw a diagram representing all the forces that act on this "system".
Example:
Example:
4) Decide which directions you are going to call "positive", by drawing the axes you choose near the free body diagram.
In our example:
In our example:
5) Write down Newton's 2nd law in terms of components, for your specific object:
- for as many directions as there are in the problem ( Σ Fx = m . ax , and / or Σ Fy = m . ay )
- Use the free body diagram and the axes from 4) to replace Σ Fx and / or Σ Fy by expressions that involve the particular forces that act on your specific object.
Example:
Σ Fy = m . ay
m g = m . ay
m g = m . ay
The corresponding steps for the angular version of Newton's 2nd law are:
1) Write down Σ τ→ = I . α→
3) Draw a free body diagram: i.e. draw a diagram representing all the forces that act on this "system".
Now you need to draw the arrows representing the forces with their tail where the force acts. For weight, that's at the center of mass of the object (i.e. at the center of the object if its density is the same throughout the object, i.e. uniform).
Example:
Now you need to draw the arrows representing the forces with their tail where the force acts. For weight, that's at the center of mass of the object (i.e. at the center of the object if its density is the same throughout the object, i.e. uniform).
Example:
4a) Decide which direction you are going to call "positive", by drawing a counterclockwise (or clockwise) arrow near the free body diagram.
There is no right or wrong decision, this is arbitrary. However, it makes calculations simpler if the direction that you choose as the positive is the direction of the angular acceleration of your object (if it has one).
Example:
4b) Decide which point you are going to choose as the pivot point.
Example:
5) Use:
- the free body diagram
- the direction from 4a)
- and the pivot point from 4b)
in order to replace Σ τ in Σ τ= I α by an expression that involves the particular forces that act on your specific object.
There is no right or wrong decision, this is arbitrary. However, it makes calculations simpler if the direction that you choose as the positive is the direction of the angular acceleration of your object (if it has one).
Example:
4b) Decide which point you are going to choose as the pivot point.
Example:
5) Use:
- the free body diagram
- the direction from 4a)
- and the pivot point from 4b)
in order to replace Σ τ in Σ τ= I α by an expression that involves the particular forces that act on your specific object.
Example:
Σ τ = I . α
SUMMARY OF DIFFERENCES BETWEEN THE ANGULAR AND THE LINEAR CASE:
- The forces on the free body diagram must be drawn with the tail of the arrow at the point where the force acts.
- The choice of a positive direction refers to either clockwise or counter-clockwise, rather than to choosing axes.
- In addition to choosing a positive direction, you now need to choose a pivot point as well.
- You need to find an expression for each of the (non-0) torques, instead of for each of the (non-0) components of the forces.
Steps 4b) and 5) are those that you are going to find new and most difficult, even if you are comfortable with applying the usual, linear version of Newton's 2nd law. So let's discuss them in detail.
Σ τ = I . α
+ mg . (d/2) cos θ = I α
SUMMARY OF DIFFERENCES BETWEEN THE ANGULAR AND THE LINEAR CASE:
- The forces on the free body diagram must be drawn with the tail of the arrow at the point where the force acts.
- The choice of a positive direction refers to either clockwise or counter-clockwise, rather than to choosing axes.
- In addition to choosing a positive direction, you now need to choose a pivot point as well.
- You need to find an expression for each of the (non-0) torques, instead of for each of the (non-0) components of the forces.
Steps 4b) and 5) are those that you are going to find new and most difficult, even if you are comfortable with applying the usual, linear version of Newton's 2nd law. So let's discuss them in detail.
DIFFICULT STEPS:
DETAILED EXPLANATIONS AND EXAMPLES
How to choose the pivot point (i.e. step 4b above)
There is no correct nor incorrect pivot point in the sense that the angular form of Newton's 2nd law would apply to the former and not to the latter. The law is true for all points, that is for any point that we may choose as the pivot point. This is the angular equivalent of the fact that Newton's (linear) 2nd law is true in all directions, i.e. whatever we choose to pick as x or y.
However, just like for Newton's linear 2nd law we did not choose directions randomly, but chose those that we knew would make solving the problem easier. The same goes for the angular version of Newton's 2nd law.
Recall that in the linear case, if the acceleration of the object was non-0, we usually chose one of the directions to be the direction of the linear acceleration. This was because it made the acceleration 0 in the direction normal (perpendicular) to that one (we'd pick x in the direction of the acceleration so that ay would be 0). Something similar goes in the angular case. As we will see in greater detail below when we discuss lever arms, what a torque turns out to be depends both on what force gives rise to it, and on where that force acts. It so happens that when a force acts directly on the pivot point (or the axis) considered, the corresponding torque is 0. This gives us a neat way of getting rid of some of the torques. To avoid having a torque appear in an equation, we just choose to apply Newton's (angular) 2nd law using as pivot point the point where the corresponding force acts.
Example:
The forces on your object of interest are:
But if instead you want the torques due to N and f to not appear in the equation (say, you are asked for the tension T and given W), then choose the point where N and f act as the pivot point:
And if it is W and its torque that you don't want to see appear, choose the point where W acts (i.e. the center of mass) to be the pivot point.
So when:
- you are not interested in finding a certain torque or the force it is due to, and:
- you know it is going to be the most difficult one to find (usually, because you don't know what the corresponding force is),
- or there are several forces acting on the same point and you are not interested in finding any of them or their torques,
it is usually a good idea to pick the point where it/they act to be the pivot point.
Note that you can apply Newton's (angular) 2nd law about several pivot points in the same problem, generating a different equation every time. In the same way that in the linear case, you can generate as many different equations as there are dimensions in the problem (i.e. in 2 dimensions, one equation for x and another for y), in the angular case, you can generate as many different, useful equations as there are points on which forces act. That doesn't mean you will need them all to solve the problem, but depending on the situation you might, or you might need several of them.
How to find the correct expression for the sum of the torques Σ τ (i.e. step 5 above):
Recall that the idea is to find the sum of the torques Σ τ in order to replace it in Σ τ= I α.
So you need to find the correct expression for each (non-0) torque, and add them all up.
The sign of the torque depends on 3 things: the direction of the force, the pivot point you chose, the direction you chose as positive.
Concretely, look at the diagram focusing your attention on only the force and the pivot point, ignoring everything else. Ask yourself in which direction that force would make your object spin about that pivot point. Once you "see" that direction, check whether that is the same direction as the one you chose as the positive one. If it is, this torque is negative (with your choice of what constitutes positive!).
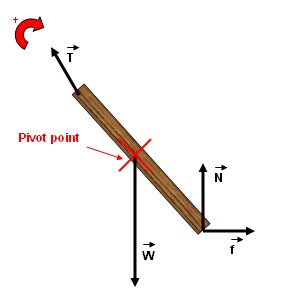
Example:
With the pivot point and choice of positive direction indicated:
- the torque due to T is 0.
- the torque due to W is negative.
- the torque due to N is positive.
- the torque due to f is positive.
Now take a piece of paper and write down whether the torques due to T, W, N and f are positive, negative or 0 in the following case:
Now check your answers by highlighting the lines below with your mouse:
- the torque due to T is negative.
- the torque due to W is positive.
- the torque due to N is 0.
- the torque due to f is 0.
Now write down whether the torques due to T, W, N and f are positive, negative or 0 in the following case (careful: the choice of positive direction has been changed too, for variety):
Now check your answers by highlighting the lines below with your mouse:
- the torque due to T is positive.
- the torque due to W is 0.
- the torque due to N is negative.
- the torque due to f is negative.
b) write down the magnitude of the force that gives rise to the torque. This step's easy. In the expression taken above as an example, + mg (d/2) cos θ , this is just mg (or W for weight if you prefer).
c) figure out what the lever arm is for this torque. In + mg (d/2) cos θ, that would be (d/2) cos θ, but figuring this out is usually the toughest part.
In order to be able to do this, the first thing you need to do, before you even begin trying to figure out the lever arms, is to write down on your diagram expressions for the lengths that you can express in terms of the one given to you, and the angle given to you.
Example:
You are given:
The first thing you must do is write down on your diagram what is added below in red:
What is the lever arm?
So you need to find the correct expression for each (non-0) torque, and add them all up.
The definition of a torque is that it is the cross-product: r→x F→. There are several methods to find the expression that this leads to. The one I am going to present here involves finding a distance called the lever arm (c) below).
There is a + sign in front if the corresponding force tends to make the object spin in the direction that you chose to be positive, and negative otherwise. Be careful however: what the torque tends to do depends not only on the force, but also on the pivot point that you chose in 4b.
Whatever method you use to find it, the expression for the torque has the following structure:
In this expression, the expression (d/2) cos θ is the lever arm, which is itself a distance. In the example given, it is not the same distance that appears explicitly, i.e. (d/2) because it must be given in terms of a distance the problem tells you about, i.e. d here.
In order to find this expression you need to:
In order to find this expression you need to:
a) figure out whether the torque is positive or negative with your choice of a positive direction in 4a. That is, decide whether the expression has a + or a - sign in front.
The sign of the torque depends on 3 things: the direction of the force, the pivot point you chose, the direction you chose as positive.
Concretely, look at the diagram focusing your attention on only the force and the pivot point, ignoring everything else. Ask yourself in which direction that force would make your object spin about that pivot point. Once you "see" that direction, check whether that is the same direction as the one you chose as the positive one. If it is, this torque is negative (with your choice of what constitutes positive!).
Example:
With the pivot point and choice of positive direction indicated:
- the torque due to T is 0.
- the torque due to W is negative.
- the torque due to N is positive.
- the torque due to f is positive.
Now take a piece of paper and write down whether the torques due to T, W, N and f are positive, negative or 0 in the following case:
Now check your answers by highlighting the lines below with your mouse:
- the torque due to T is negative.
- the torque due to W is positive.
- the torque due to N is 0.
- the torque due to f is 0.
Now write down whether the torques due to T, W, N and f are positive, negative or 0 in the following case (careful: the choice of positive direction has been changed too, for variety):
Now check your answers by highlighting the lines below with your mouse:
- the torque due to T is positive.
- the torque due to W is 0.
- the torque due to N is negative.
- the torque due to f is negative.
b) write down the magnitude of the force that gives rise to the torque. This step's easy. In the expression taken above as an example, + mg (d/2) cos θ , this is just mg (or W for weight if you prefer).
c) figure out what the lever arm is for this torque. In + mg (d/2) cos θ, that would be (d/2) cos θ, but figuring this out is usually the toughest part.
In order to be able to do this, the first thing you need to do, before you even begin trying to figure out the lever arms, is to write down on your diagram expressions for the lengths that you can express in terms of the one given to you, and the angle given to you.
Example:
You are given:
The first thing you must do is write down on your diagram what is added below in red:
What is the lever arm?
The lever arm is the shortest distance between the direction of the force (i.e. a line going through the force) and the pivot point.
So be aware that the lever arm depends on both the direction of the force whose torque you are after, and the pivot point that you chose.
Concretely, look at the diagram focusing your attention on only the force and the pivot point, ignoring everything else (yep, so far it's like what you did to find the sign of the torque).
Now imagine a straight line going through the force. Then imagine the shortest line segment between that line and the pivot point. Once you "see" it, identify what its length must be in terms of the distances given in the problem.
Example:
You want to find lever arms for the non-0 torques in the following situation:
To find the lever arm for the torque due to N, these are the elements that you must focus on, and this is the lever arm that you should imagine:
This implies that for the torque due to N the lever arm is equal to (L/2) cos θ:
If you have trouble understanding why, picture the following:
and look at the first rule on this link.
Ok so that was for the lever arm associated with N. Now ponder the diagram below and write down on a piece of paper what the lever arm is for f:
Now check your answer by highlighting the line below with your mouse:
(L/2) sin θ
If you still can't see it, ponder this diagram:
How about W? What is the lever arm for W?
Write it down on a piece of paper.
Now check your answer by highlighting the lines below with your mouse:
So be aware that the lever arm depends on both the direction of the force whose torque you are after, and the pivot point that you chose.
Concretely, look at the diagram focusing your attention on only the force and the pivot point, ignoring everything else (yep, so far it's like what you did to find the sign of the torque).
Now imagine a straight line going through the force. Then imagine the shortest line segment between that line and the pivot point. Once you "see" it, identify what its length must be in terms of the distances given in the problem.
Example:
You want to find lever arms for the non-0 torques in the following situation:
To find the lever arm for the torque due to N, these are the elements that you must focus on, and this is the lever arm that you should imagine:
If you have trouble understanding why, picture the following:
and look at the first rule on this link.
Ok so that was for the lever arm associated with N. Now ponder the diagram below and write down on a piece of paper what the lever arm is for f:
Now check your answer by highlighting the line below with your mouse:
(L/2) sin θ
If you still can't see it, ponder this diagram:
How about W? What is the lever arm for W?
Write it down on a piece of paper.
Now check your answer by highlighting the lines below with your mouse:
It is 0. The shortest distance between the direction of W and the pivot point is 0, since W acts directly on the pivot point (usually chosen by you). This is why the torque due to a force that acts on the pivot point/axis is 0.
And what about T? What is the lever arm associated with it?
It is 0 as well! Indeed, the line that goes through T goes through the pivot point, so the shortest distance between that line and the pivot point is once again 0. It is not only torques from forces that act on the pivot point that are 0: the torque due to any force whose direction goes through the pivot point is also 0!
Remember this if you have trouble choosing a pivot point that works for your problem using the simplest rule given above!
In the previous section, we chopped the difficult steps up into small bits in order to explain them in detail. In this section, we work out a full example, without going into explanations as to why the answers are what they are - that's in the previous section!
You need to do this along, so grab a nice piece of paper and your favorite pen ;-)
You are given a problem that you know is going to involve you applying the angular form of Newton's 2nd law. The physical situation is the following. A firefighter stands on a uniform ladder of length L, a third of the way from the top of the ladder. The ladder is standing on a frictionless floor, at an angle θ to the floor. It is leaning against a wall. The friction coefficient between the wall and the ladder is non-0. Everything is going well at the moment of interest: neither firefighter nor ladder are accelerating! They give you this drawing to go with:
Do step 1: write down the relevant law in its most general form.
Now check your answer by highlighting the line below with your mouse:
Σ τ→ = I . α→
Do step 2: decide what object you want to apply this law to.
Now check your answer by highlighting the lines below with your mouse:
Considerable experience with homework problems makes it clear to you that you want to apply the law to the ladder.
Do step 3: draw the free body diagram (don't peek!).
Now check your answer by scrolling down:
Note that we have indicated the weight of the firefighter on the free body diagram. This is a sloppy habit that most physicists have taken, in fact this force is a normal force: the normal force exerted by the firefighter's feet on the ladder. This normal force so happens to be equal in magnitude and direction to the firefighter's weight when (s)he isn't accelerating, hence the sloppy habit.
Step 4a, i.e. choosing a positive direction, I am going to impose, so you can end up with the same equation as I have below. I am choosing counter-clockwise.
Draw it on your diagram!
Do step 4b, i.e. choose a pivot point, such that you can make the greatest number of torques equal to 0.
Write down your answer.
Check it by highlighting the lines below with your mouse:
For that you must choose the point of contact between the ladder and the wall as the pivot point. Two forces are exerted there (the normal force due too the wall and the friction force due to the wall). No other point has more forces applied on it, and no point has more forces having directions going through it, either.
Do step 5. First, add onto your diagram everything else that you need to do this (again, don't peek!).
Now check your answer by scrolling down. Your diagram should look like what is below:
Now write down the angular version of Newton's second law, for these choices of positive direction and pivot point.
After you have written all of it down, check your answer by highlighting the lines below with your mouse:
- NG . L cos θ + ML g . (L/2) cos θ + MF g . (L/3) cos θ = 0
We have set the right hand side to 0 because the ladder has no angular acceleration (as usual in "statics" problems).
Compare what you wrote down to this answer!
- If you got some of the signs wrong, and you can't immediately see why, study the relevant part in the previous section. That's the one that starts with:
"a) figure out whether the torque is positive or negative with your choice of a positive direction in 4a. That is, decide whether the expression has a + or a - sign in front."), under the colorful expression.
- If you got wrong some of the expressions involving either L or cos and sin, and you can't immediately see why, study the relevant part in the previous section. That's the one that starts with:
"c) figure out what the lever arm is for this torque. In + mg (d/2) cos θ, that would be (d/2) cos θ, but figuring this out is usually the toughest part."
More practice:
Now write down the angular version of Newton's second law, for the choices of positive direction and pivot point below:
After you have written all of it down, check your answer by highlighting the line below with your mouse:
ML g . (L/2) cos θ + MF g . (2L/3) cos θ - Nw . L sin θ - f . L cos θ = 0
Now write down the angular version of Newton's second law, for the choices of positive direction and pivot point below:
After you have written all of it down, check your answer by highlighting the line below with your mouse:
NG . (L/2) cos θ + MF g . (L/6) cos θ - Nw . (L/2) sin θ - f . (L/2) cos θ = 0
Now write down the angular version of Newton's second law, for the choices of positive direction and pivot point below:
After you have written all of it down, check your answer by highlighting the line below with your mouse:
- NG . (2L/3) cos θ + ML g . (L/6) cos θ + Nw . (L/3) sin θ + f . (L/3) cos θ = 0
And what about T? What is the lever arm associated with it?
Write it down on a piece of paper.
Now check your answer by highlighting the lines below with your mouse:
Now check your answer by highlighting the lines below with your mouse:
It is 0 as well! Indeed, the line that goes through T goes through the pivot point, so the shortest distance between that line and the pivot point is once again 0. It is not only torques from forces that act on the pivot point that are 0: the torque due to any force whose direction goes through the pivot point is also 0!
Remember this if you have trouble choosing a pivot point that works for your problem using the simplest rule given above!
MORE PRACTICE / DIAGNOSTIC EXAMPLE
In the previous section, we chopped the difficult steps up into small bits in order to explain them in detail. In this section, we work out a full example, without going into explanations as to why the answers are what they are - that's in the previous section!
You need to do this along, so grab a nice piece of paper and your favorite pen ;-)
You are given a problem that you know is going to involve you applying the angular form of Newton's 2nd law. The physical situation is the following. A firefighter stands on a uniform ladder of length L, a third of the way from the top of the ladder. The ladder is standing on a frictionless floor, at an angle θ to the floor. It is leaning against a wall. The friction coefficient between the wall and the ladder is non-0. Everything is going well at the moment of interest: neither firefighter nor ladder are accelerating! They give you this drawing to go with:
Do step 1: write down the relevant law in its most general form.
Now check your answer by highlighting the line below with your mouse:
Σ τ→ = I . α→
Do step 2: decide what object you want to apply this law to.
Now check your answer by highlighting the lines below with your mouse:
Considerable experience with homework problems makes it clear to you that you want to apply the law to the ladder.
Do step 3: draw the free body diagram (don't peek!).
Now check your answer by scrolling down:
Note that we have indicated the weight of the firefighter on the free body diagram. This is a sloppy habit that most physicists have taken, in fact this force is a normal force: the normal force exerted by the firefighter's feet on the ladder. This normal force so happens to be equal in magnitude and direction to the firefighter's weight when (s)he isn't accelerating, hence the sloppy habit.
Step 4a, i.e. choosing a positive direction, I am going to impose, so you can end up with the same equation as I have below. I am choosing counter-clockwise.
Draw it on your diagram!
Do step 4b, i.e. choose a pivot point, such that you can make the greatest number of torques equal to 0.
Write down your answer.
Check it by highlighting the lines below with your mouse:
For that you must choose the point of contact between the ladder and the wall as the pivot point. Two forces are exerted there (the normal force due too the wall and the friction force due to the wall). No other point has more forces applied on it, and no point has more forces having directions going through it, either.
Do step 5. First, add onto your diagram everything else that you need to do this (again, don't peek!).
Now check your answer by scrolling down. Your diagram should look like what is below:
Now write down the angular version of Newton's second law, for these choices of positive direction and pivot point.
After you have written all of it down, check your answer by highlighting the lines below with your mouse:
- NG . L cos θ + ML g . (L/2) cos θ + MF g . (L/3) cos θ = 0
We have set the right hand side to 0 because the ladder has no angular acceleration (as usual in "statics" problems).
Compare what you wrote down to this answer!
- If you got some of the signs wrong, and you can't immediately see why, study the relevant part in the previous section. That's the one that starts with:
"a) figure out whether the torque is positive or negative with your choice of a positive direction in 4a. That is, decide whether the expression has a + or a - sign in front."), under the colorful expression.
- If you got wrong some of the expressions involving either L or cos and sin, and you can't immediately see why, study the relevant part in the previous section. That's the one that starts with:
"c) figure out what the lever arm is for this torque. In + mg (d/2) cos θ, that would be (d/2) cos θ, but figuring this out is usually the toughest part."
More practice:
Now write down the angular version of Newton's second law, for the choices of positive direction and pivot point below:
After you have written all of it down, check your answer by highlighting the line below with your mouse:
ML g . (L/2) cos θ + MF g . (2L/3) cos θ - Nw . L sin θ - f . L cos θ = 0
Now write down the angular version of Newton's second law, for the choices of positive direction and pivot point below:
After you have written all of it down, check your answer by highlighting the line below with your mouse:
NG . (L/2) cos θ + MF g . (L/6) cos θ - Nw . (L/2) sin θ - f . (L/2) cos θ = 0
Now write down the angular version of Newton's second law, for the choices of positive direction and pivot point below:
After you have written all of it down, check your answer by highlighting the line below with your mouse:
- NG . (2L/3) cos θ + ML g . (L/6) cos θ + Nw . (L/3) sin θ + f . (L/3) cos θ = 0